L'Optimisation Combinatoire consiste à trouver la meilleure solution parmi un nombre fini (mais souvent très grand) de choix. C'est une branche de la « Programmation Mathématique » qui recouvre les méthodes qui servent à déterminer l'optimum d'une fonction sous des contraintes données. Il s'agit donc de minimiser une fonction sur un ensemble fini, mais éventuellement très grand, et dont les propriétés mathématiques ne sont pas facilement caractérisables. La recherche de ces caractérisations, et des algorithmes d'optimisation qui les utilisent, constitue l'essentiel du travail de l'équipe. Nous nous basons sur notre expertise pour cerner de nouveaux problèmes, théoriques ou appliqués, et les analyser pour en extraire les propriétés fondamentales qui permettront de les résoudre ou de montrer que leur résolution est difficile. De plus, nous utilisons et développons des outils théoriques qui permettent de traiter ces problèmes avec des méthodes appropriées (exactes, heuristiques, algorithmes d'approximation, etc), qui peuvent être « ad hoc » ou « génériques ».
Grâce aux résultats obtenus et aux activités qui en découlent - séminaires, projets internationaux, exposés et cours, accueil d'un grand nombre de jeunes chercheurs - Grenoble est un centre attractif du domaine et plus généralement des mathématiques discrètes.
Pour les problèmes les plus difficiles de l'optimisation combinatoire, la solution algorithmique est souvent précédée de théorèmes qui révèlent la structure du problème, ou qui donnent une « bonne caractérisation », notion clé qui permet de justifier la réponse. Nous développons aussi bien ces théorèmes que leurs conséquences algorithmiques, ou des résultats négatifs qui nous permettent de construire des algorithmes d'approximation. Sur un plan purement théorique, nous nous intéressons à des objets mathématiques dont les solutions contribuent à une bibliothèque de connaissances prête à être utilisée le moment venu. Ainsi, nous travaillons sur la théorie des couplages (T-joins, maxfix covers), les chemins disjoints dans les graphes (routage, multiflots), ou des problèmes de packing et covering.
Sur un plan plus appliqué, nous traitons aussi des problèmes théoriquement difficiles comme le « problème du voyageur de commerce » ou ses variantes, comme le « routage des véhicules ». Pour ces problèmes, l'approche polyédrale est privilégiée et des techniques branch and cut développées.
La combinatoire s'est forgée ses propres méthodes qui peuvent aussi faire appel à des outils avancés des mathématiques classiques. De nombreux exemples montrent qu'un outil d'algèbre linéaire, ou de théorie des nombres, ou encore un outil géométrique y compris la programmation en nombres entiers, peut débloquer la solution d'un problème difficile. Les preuves construites ainsi sont souvent simples et élégantes, et conduisent, pour certaines à des résultats fondamentaux et algorithmiquement efficaces. Un outil, qui s'est révélé très puissant est basé sur une idée originale : à un objet combinatoire (par exemple des couplages, des parcours de voyageurs ou des tournées de véhicules), on peut associer un vecteur - souvent le vecteur naturel « d'incidence » de l'objet. Optimiser sur les objets voulus revient à optimiser sur leur enveloppe convexe par des propriétés de base de la programmation linéaire. Ceci est l'idée de départ de la Combinatoire Polyédrale.
 |
 |
 |
En revanche les contraintes de cette enveloppe convexe ne sont pas nécessairement faciles à déterminer. Cela constitue un sujet de recherches théoriques et appliquées important, conduisant souvent à des problèmes linéaires en nombres entiers. L'équipe contribue à ces recherches, par exemple par l'étude des cônes hilbertiens, des nombres de Carathéodory, ou encore par l'étude d'une conjecture de Berge et Linial sur la couverture des sommets d'un graphe par des cycles. Ces travaux amènent parfois au développement d'algorithmes branch and cut pour la détermination de solutions optimales. Par exemple, les « noyaux » dans les graphes conduisent à des résultats topologiques de Scarf, en lien aussi avec la théorie des jeux. Les « clutters binaires », une généralisation abstraite des « espaces de circuits » des graphes, ont permis de résoudre une grande variété de problèmes (concernant les tournées de postiers, les multiflots, ...) et d'avancer sur le problème de « paintshop scheduling », problème d'ordonnancement de production de l'industrie automobile qui consiste à optimiser la séquence de peinture d'une série de voitures.
Nous nous intéressons aux aspects structurels, algorithmiques et extrémaux des graphes.
Les problèmes d'optimisation étudiés impliquent souvent les graphes, en lien avec des notions comme les colorations, flots, couplages, T-joints, tours, et arborescences. Les graphes eux-mêmes peuvent contenir des informations supplémentaires à prendre en compte, comme une métrique sous-jacente, un plongement dans une surface ou plus généralement dans un espace topologique. La résolution des problèmes mobilise de nombreux outils provenant de la théorie des graphes et l'optimisation combinatoire, comme par exemple les matroïdes, les fonctions sous-modulaires, la combinatoire polyédrale et la programmation linéaire (éventuellement en nombres entiers), la programmation semi-définie, mais aussi des outils de probabilités, topologie, géométrie, algèbre linéaire et théorie des groupes.
Lorsque le graphe est très grand, on ne peut pas se permettre d'utiliser des algorithmes exacts classiques car une complexité quadratique (voire linéaire) est déjà bloquante. On peut alors vouloir sacrifier un peu de précision pour réduire drastiquement la complexité, visant alors un temps sous-linéaire. C'est l'approche suivie dans le cadre du Property Testing : étant donnés une propriété P et un graphe G, on veut décider très efficacement si G vérifie la propriété P, ou bien s'il est "loin" de la vérifier (laissant indécis le cas transitoire où G échoue de peu à satisfaire P). Par exemple, décider si le graphe est loin d'être sans triangle a des liens forts avec des problèmes de combinatoire additive et le lemme de régularité de Szemerédi.
Nous utilisons les avancées sur les aspects structurels ou extrémaux pour développer des algorithmes efficaces pour résoudre des problèmes d'optimisation discrète. En plus de la question de l'existence d'une solution à un certain problème, on peut s'intéresser à l'ensemble des solutions à ce problème: soit en désirant toutes les énumérer de manière rapide, soit en essayant de comprendre la géométrie de l'espace des solutions (est-il possible de passer de n'importe quelle solution à n'importe quelle solution par une suite de petites modifications locales?). Cela motive en particulier les thématiques de l'énumération et de la reconfiguration combinatoire sur lesquelles plusieurs membres de l'équipe travaillent, et qui sont en lien avec des questions en physique statistique notamment, et nécessitent parfois des outils avancés de topologie.
Les graphes étudiés sont parfois plongés dans des espaces métriques (problème du Voyageur de Commerce) ou topologiques (plongements planaires ou sur une surface par exemple), ou ont des propriétés algébriques exceptionnelles (graphe de Cayley...), et les techniques algorithmiques doivent prendre en compte ces structures additionnelles. Les techniques développées se rapprochent alors davantage de la géométrie, de la topologie, ou de la théorie des groupes, que des méthodes combinatoires usuelles.
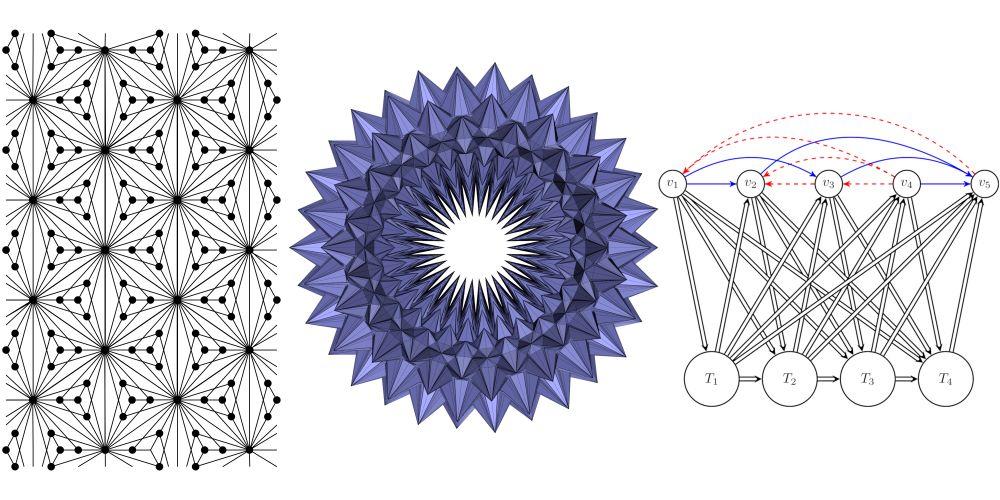
Voici quelques illustrations :
En plus de l'étude théorique des problèmes combinatoires et de leur complexité algorithmique, l'équipe s'intéresse à l'utilisation de la programmation mathématique pour résoudre des problèmes industriels de grande taille, à l'aide notamment de la programmation linéaire en nombres entiers, de la génération de colonnes, et des relaxations lagrangiennes. Ces applications sont mises en œuvre en partie lors du co-encadrement de thèses CIFRE avec des partenaires industriels.
